Für das nachfolgende System 3. Ordnung, bestehend aus el. Widerständen und Kondensatoren, liegt ein Zustandsraummodell vor.
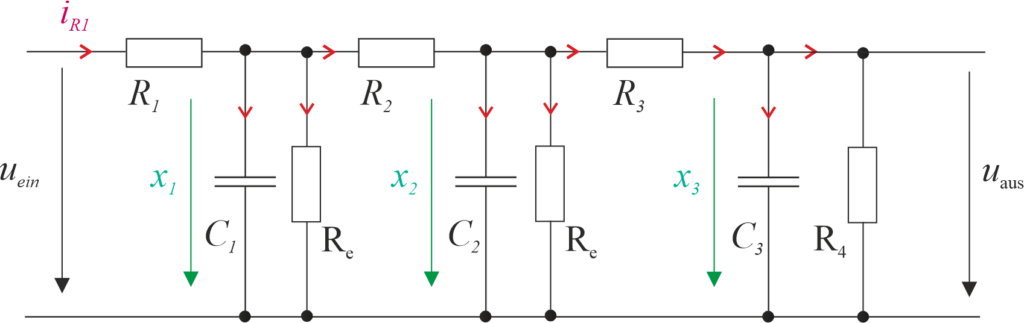
Die Bauteile genügen den Bedingungen:
\[ R_1 = R_2 = R_3= R \quad R_4 = R_e \quad C_1 = C_2 = C_3 = C \quad \quad T = RC \]Das Zustandsraummodell der RC-Schaltung ist:
\[ \left[ \begin{array}{c} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \end{array} \right] = \begin{bmatrix} -(2/T+1/(CR_e)) & 1/T & 0\\ 1/T & -(2/T+1/(CR_e) ) & 1/T \\ 0 & 1/T & -(1/T+1/(CR_e))\end{bmatrix} \left[ \begin{array}{c} x_1 \\ x_2 \\ x_3\end{array} \right] + \left[ \begin{array}{c} 1/T \\ 0 \\ 0\end{array} \right] u_{ein}\]Das Modell wird in Python mit Bauteildaten wie folgt dargestellt
import numpy as np
import control as ct
import matplotlib.pyplot as plt
# Regelstrecke in Zustandsraumdarstellung
C = 100e-6 # Kond
R = 10e3 # Widerstand 1, 2 und 3
Re = 1200e3 # Rein ADW 1,2M
R4 = 100e3 # Widerstand 4
T = R*C
T2 = C*Re
Am = np.array([[-(2/T + 1/T2), 1/T, 0],
[1/T, -(2/T + 1/T2), 1/T],
[0, 1/T, -(1/T + 1/(Re*C))]])
bm = np.array([[ 1/T],[0],[0]])
cmt = np.array([ [0], [0], [1]]) # transponierter Ausgangsvektor für Ackermannformel
CC = np.identity(3)
D = np.zeros((3,1))
RC3 = ct.ss(Am, bm, CC, D, name='rc3',inputs='u', outputs=['y1','y2','y3'])
Der Entwurf des Beobachters setzt die Vorgabe der Dynamik voraus (siehe im Buch ab S. 256).
# Beobachterentwurf p = -1/0.7 # Vorgabe Dynamik/Pole # Rückkoppelvektor mit Hilfe der Formel von Ackermann berechnen h = ct.acker(Am,cmt,[p,p,p]) # Bildung Eingangsmatrix Beobachter bo = np.zeros((3,2)) bo[:,0]=bm.T bo[:,1]=h DD = np.zeros((3,2)) #Beobachtermodell bmod = ct.ss(Am, bo, CC, DD, name='beob',inputs=['u','e'], outputs=['x1','x2','x3'])
Für die Simulation werden Strecke und Beobachter zusammengeführt:
# Bildung Fehlersignal
sumblk = ct.summing_junction(inputs=['y3', '-x3'], output='e')
# Strecke mit Beobachter
Sb = ct.interconnect([RC3,sumblk, bmod
], inplist='u', outlist=['y1','y2','y3','x1','x2','x3','e'])
t=np.arange(0,30,0.05)
ww = np.ones(len(t))
x0 = [0.4,0.4,0.4,0,0,0] # Vorgabe Anfangswerte
t, yy = ct.input_output_response(Sb, t, ww,x0,solve_ivp_method='BDF')
plt.figure()
plt.plot(t,yy.T)
plt.title('Beobachter für RC3R')
plt.xlabel('t [s]'); plt.ylabel('alle x')
plt.grid()
#plt.figure() # plot step x ohne Beobachter
#plt.plot(t,y[:,0,:].T)
# Diskretisierung Beobachter
modd = ct.c2d(bmod,0.1)
print(modd)
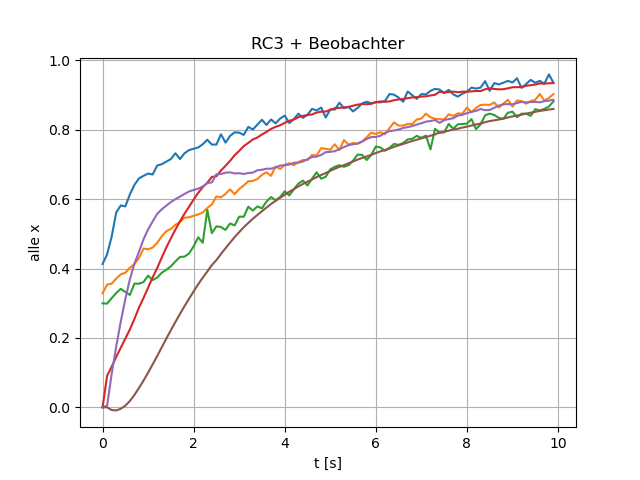
Das nachfolgende Bild zeigt die Sprungantwort aller Zustände der Strecke mit Beobachter. Die Strecke wurde mit gleichen Anfangswerten versehen (0,4), der Beobachter (Anfangswerte alle 0) schätzt aber nach ca. 5 Sek. alle Zustände korrekt. Die Vorgabe einer schnelleren Beobachterdynamik (z.B. mit p =-1/0,4) verbessert das Verhalten deutlich.

Ein Beobachter wird in der Praxis nicht so glatte Zeitverläufe aufweisen, jedoch die Zustände gut schätzen können. Das folgende Beispiel zeigt die gemessenen Werte des RC-Netzwerks und die Reaktion des Beobachters, der mit microPython auf einem esp32 realisiert wurde. Die Zustände des RC-Netzwerks starten bei ca. 0,4 Volt, die Beobachterzustände starten bei 0 Volt.