Die Simulation nicht linearer Systeme mit der Python Control System Library wird durch neue Funktionen der Version 0.9 vom März 2021 erleichtert (R. M. Murray). Hier ist die interconnect-Funktion zu nennen, die eine Kopplung von einzelnen ioSystemen auf Basis von Signalnamen ermöglicht. Eine graphische Programmierung, wie es Simulink oder WinFact ermöglicht, ist damit nicht möglich, aber vorgefertigte “Blöcke“ in Form von “input/output systems“ können einfacher miteinander verbunden werden. Der Nachteil einer rein textbasierten Beschreibung von Systemen kann dadurch etwas ausgeglichen werden.
Ein ioSystem kann linear ( LinearIOSystem(ss_sys) ) oder nicht linear ( NonlinearIOSystem(updfcn, outfcn, inputs=, outputs=, states=) ) sein.
Da Regelkreise aufgrund der stets vorhandenen Begrenzung der Stellgröße nicht linear sind und ein praxisnaher PI-Regler eine Anti-Windup-Funktion enthalten sollte, sind nicht lineare Simulationsfunktionen erforderlich. Input/Output-Systeme können eine Update-Funktion (updfcn) aufweisen, die die Ableitungsfunktionen der einzelnen Zustände aufweist. Eine Output-Funktion (outfcn) kann auf Grundlage der Zustände und Eingänge eine Ausgangsgröße bilden. Die Zustandsraumbeschreibung hilft beim Verständnis der Funktion NonlinearIOSystem() In WinFact/Boris finden wir mit dem benutzerdefinierten Dgl.-System eine analoge Funktion.
Wie in Python üblich müssen die Funktionen mit dem Befehl “def“ definiert werden. Z.B. die Update-Funktion für einen PI-Regler mit Anit-Windup:
def pi_update(t, x, u, params={}):
# Reglerparameter übergeben, falls erforderlich
kp = params.get('kp', 0.5)
Tn = params.get('Tn', 1.0)
ki = kp/Tn
Tikor = 0.9*Tn # Anti-Windup-Korrekturfaktor
ybeg = params.get('ybeg', 2.0)
# Zuweisung von Variablen und Zuständen
e = u # Regelfehler
ei = x[0] # Zustand korr. integrierter Regelfehler
# Berechnete Stellgröße ohne Begrenzung
y_a = pi_output(t, x, u, params)
# Berechnung Anti-Windup-Kompensation
e_kor = (np.clip(y_a, -ybeg, ybeg) - y_a)/(ki*Tikor) if Tn != 0 else 0
return e + e_kor # eiPunkt = e + e_kor
Die Output-Funktion eines IO-Systems hat diesen beispielhaften Aufbau:
def pi_output(t, x, u, params={}):
# Reglerparameter übergeben, falls erforderlich
kp = params.get('kp', 0.5)
Tn = params.get('Tn', 1.0)
ybeg = params.get('ybeg', 2.0)
ki = kp/Tn
# Zuweisung von Variablen und Zuständen
e = u # Regelfehler
ei = x[0] # integrierter korr. Regelfehler
# PI Reglerstellgröße mit AWR
return kp * e + ki*ei
Das IO-System kann nun wie folgt erstellt werden:
import control as ct
io_PI_awr = ct.NonlinearIOSystem( pi_update, pi_output, name='control',
inputs = ['e'], outputs = ['yy'], states = ['ei'],
params = {'kp':0.5, 'Tn':1.0, 'ybeg':10.0})
Die Simulation benötigt den Befehl
t, yyy = ct.input_output_response(io_PI_awr, T, ww)
wobei ein Zeitvektor T und die Eingangsgrößen zur Verfügung gestellt werden müssen. Das Beispielprogramm berechnet die Ausgangsgröße yy eines PI-Reglers mit Anit-Windup, jedoch muss yy nochmals begrenzt werden, falls das Streckenmodell die Begrenzung nicht enthält. Dazu wird ein weiteres IO-System gebildet und mit der Interconnect-Funktion mit dem PI-Regler verknüpft:
def y_output(t, x, u, params={}):
ybeg = params.get('ybeg', 2.0)
# Zuweisung von Variablen und Zuständen
yy = u[0]
# nur Begrenzung
return np.clip(yy, -ybeg, ybeg)
Begrenzung = ct.NonlinearIOSystem( None, y_output, name='begrenzung',
inputs = ['yy'], outputs = ['yb'],
params = {'ybeg':10.0})
Da beide Systeme den Ausgang bzw. den Eingang gleich mit yy bezeichnen, koppelt die Interconnect-Funktion diese beiden Signale.
io_PIawrBeg = ct.interconnect([io_PI_awr, Begrenzung], inplist=[‚e‘], outlist=’yb‘)
Die Eingänge und Ausgänge des gekoppelten Systems müssen benannt werden. Interessant ist die Einbeziehung der Strecke und der Aufbau eines Regelkreises. Dafür wird die neue Funktion “summing_junction()“ verwendet, die eine Addition der Rückkopplung, hier sumblk, ermöglicht.
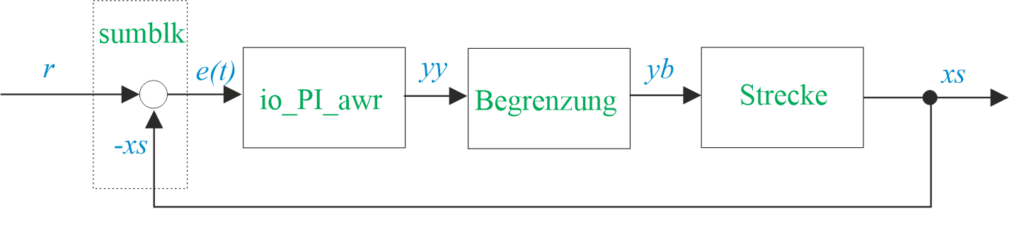
Der Wirkungsplan zeigt die Namen und Anordnung der Programmblöcke und die Namen der Verbindungen. Die Strecke wird hier als lineares System definiert:
Strecke = ct.tf2io(ct.tf(5, [0.5, 1.5, 1]), inputs=’yb‘, outputs=’xs‘)
sumblk = ct.summing_junction(inputs=[‚r‘, ‚-xs‘], output=’e‘)
Nun können alle Blöcke zusammengefügt werden:
Rk = ct.interconnect([Strecke, io_PI_awr,Begrenzung, sumblk], inplist=’r‘, outlist=[‚xs‘,’yb’])
Die Ausgangsgrößen sind die Regelgröße xs und die Stellgröße yb.
Der Regelkreis Rk kann nun simuliert werden, z.B. die Reaktion von Regelgröße und Stellgröße auf eine sprungförmige Führungsgröße.
t, yy = ct.input_output_response(Rk, T, ww)
Damit ist eine wiederverwertbare Struktur vorgestellt worden, die eine Simulation einer Strecke mit Begrenzung und PI-Regler mit AWR-Maßnahme im Grundregelkreis ermöglicht. Weitere Beispiele sind in der Programmdokumentation der Python Control System Library zu finden.
Das vollständige Programmbeispiel für die Version 0.10.1 siehe folgendes Listing 10.1:
# -*- coding: utf-8 -*-
"""
Created on 7.4. 2021, modifiziert für Version 0.10.1 am 19.8.24
PI-Regler mit AWR und Strecke mit ioSys
@author: philippsen
"""
import control as ct
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['pdf.fonttype'] = 42
plt.rcParams['ps.fonttype'] = 42
def pi_update(t, x, u, params={}):
# Reglerparameter übergeben, falls erforderlich
kp = params.get('kp', 0.5)
Tn = params.get('Tn', 1.0)
ki = kp/Tn
Tikor = 0.9*Tn # Anti-Windup-Korrekturfaktor
ybeg = params.get('ybeg', 2.0)
# Zuweisung von Variablen und Zuständen
e = u # Regelfehler
ei = x[0] # Zustand korr. integrierter Regelfehler
# Berechnete Stellgröße ohne Begrenzung
y_a = pi_output(t, x, u, params)
# Berechnung Anti-Windup-Kompensation
e_kor = (np.clip(y_a, -ybeg, ybeg) - y_a)/(ki*Tikor) if Tn != 0 else 0
return e + e_kor # eiPunkt = e + e_kor
def pi_output(t, x, u, params={}):
# Reglerparameter übergeben, falls erforderlich
kp = params.get('kp', 0.5)
Tn = params.get('Tn', 1.0)
ybeg = params.get('ybeg', 2.0)
ki = kp/Tn
# Zuweisung von Variablen und Zuständen
e = u # Regelfehler
ei = x[0] # integrierter korr. Regelfehler
# PI Reglerstellgröße mit AWR
return kp * e + ki*ei
io_PI_awr = ct.NonlinearIOSystem(
pi_update, pi_output, name='control',
inputs = ['e'], outputs = ['yy'], states = ['ei'],
params = {'kp':0.5, 'Tn':1.4, 'ybeg':10.0})
# Leider wird nicht die begrenzte Stellgröße berechnet,
# sondern die Unbegrenzte! Also nochmal begrenzen
def y_output(t, x, u, params={}):
# parameter übergeben, falls erforderlich
ybeg = params.get('ybeg', 2.0)
# Zuweisung von Variablen und Zuständen
yy = u[0]
# nur Begrenzung
return np.clip(yy, -ybeg, ybeg)
Begrenzung = ct.NonlinearIOSystem(
None, y_output, name='begrenzung',
inputs = ['yy'], outputs = ['yb'],
params = {'ybeg':10.0})
X0 = [0, 0, 0, 0,0] # Anfangswerte
T = np.arange(0.0, 10.0, 0.05) # Simulationsdauer
# Simulation Regler-Sprungantwort
io_PIawr = ct.interconnect([io_PI_awr, Begrenzung], inplist=['e'], outlist='yb')
ww = np.zeros([len(T)])
for i in range(len(T)):
if T[i] > 1:
ww[i] = 35
else:
ww[i] = 0
# Strecke
strecke = ct.tf(5, [0.5, 1.5, 1], inputs='yb', outputs='xs')
sumblk = ct.summing_junction(inputs=['r', '-xs'], output='e')
#Regelkreis aufbauen
Rk = ct.interconnect([strecke,
io_PI_awr,Begrenzung, sumblk], inplist='r', outlist=['xs','yb'])
t, yy = ct.input_output_response(Rk, T, ww)
#
# Plot Regelkreis-Sprungantwort
plt.figure(1)
plt.plot(t,yy[0,:],t,yy[1,:])
plt.xlabel('t [s]');plt.ylabel('y (rot) , x (blau)')
plt.title('Sprungantwort (t=1)')
plt.grid()
